[모두를 위한 딥러닝] 4. multi-variable linear regression

# Mulit-variable linear regression

 

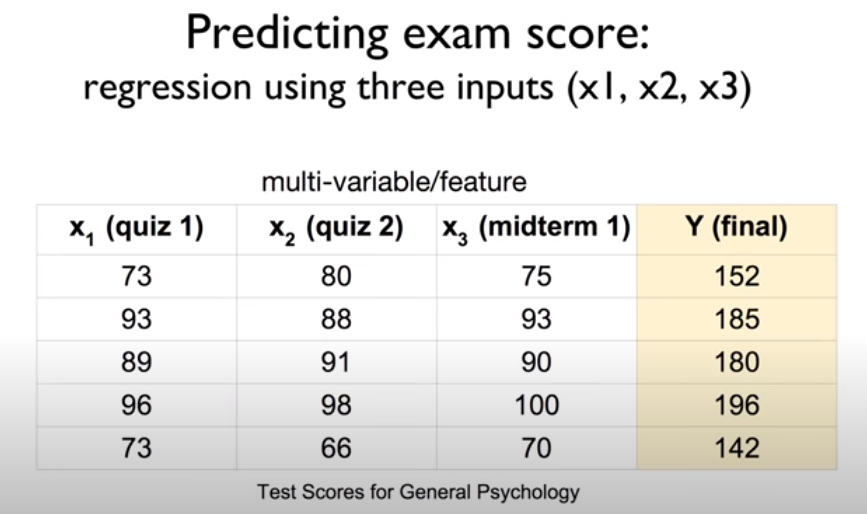
 앞에서 공부했던 선형 회귀는 하나의 변수에 대하여 출력을 계산했다. 그러나 위 시험 점수 예측 사례의 퀴즈 1 점수, 퀴즈 2 점수, 중간고사 점수처럼 여러개의 변수를 고려하여 회귀를 진행할 땐 어떻게 해야할까?

 

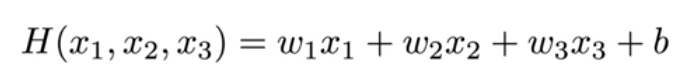
 기존의 선형 회귀 식은 H(x) = Wx + b였다. 다변량 선형 회귀는 위와 같이 기존 선형 회귀와 유사하게 새로운 가중치 w를 각각의 새로운 변수 x들에 곱해주면 된다.

 

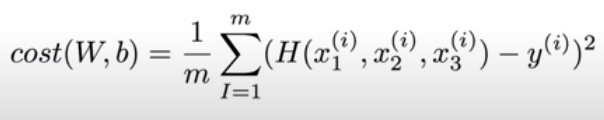
  다변량 선형 회귀의 비용함수 역시 선형 회귀의 비용함수 식을 그대로 가져오되 Hypothesis만 다변량 회귀식으로 적용하여 사용한다.

 

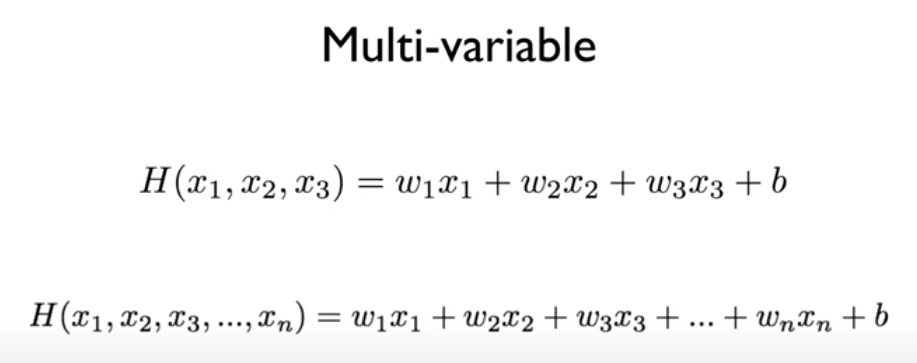
 Hypothesis를 n개의 변수에 대하여 일반화하면 위와 같다. 그러나 n의 값이 커질수록 식이 길어서 이를 표현하기 어려워지는 문제가 생긴다.

 

 식이 길어지는 문제는 행렬(Matrix)을 도입하는 방법(= Vectorization)으로 해결할 수 있다. 변수 x들에 대한 행렬 X와 각각의 변수에 대한 가중치 w들을 표현하는 행렬 W를 사용해 H(X) = XW라는 Hypothesis를 사용할 수 있다. 일반적으로 이론에 사용되는 식에서는 H(x) = Wx 처럼 W를 앞에 사용하지만, 실제로 구현할 때는 XW와 같이 X를 앞에 두고 사용한다. Vectorization은 n개의 변수에 대해 n번이나 수행되어야 하는 계산을 한번으로 줄여 효율적인 계산을 돕는 이점이 있다.

 

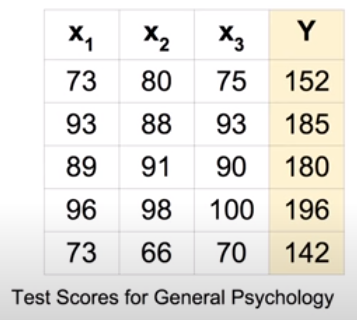
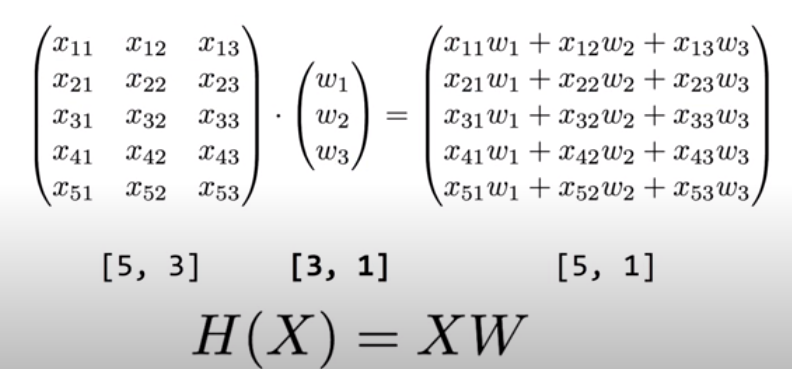
 위는 기말 시험 점수를 예측하는 다변량 선형 회귀에 대한 예시이다. 왼쪽 상단의 표에는 3가지 시험 점수 변수와 기말 점수 변수에 대한 데이터가 5개 있다. 이러한 데이터 하나하나를 Instance라고 한다. 행렬로 다변량 선형 회귀를 수행할 때는 그 행과 열에 정보가 담겨 있는데, X의 행은 instance의 개수(data의 개수), 열은 독립변수의 개수를 나타낸다. W의 행은 독립변수의 개수를 나타내며 열은 출력 개수를 나타낸다. 그리고 두 행렬 X와 W를 계산한 결과를 담는 행렬은 행이 instance의 개수, 열이 출력의 개수를 나타낸다. 

 

 

본 포스팅은 김성훈 교수님의 강의

'모두를 위한 딥러닝'을 학습하고 정리한 내용을 담고 있습니다.