[모두를 위한 딥러닝] 5. Logistic Regression

# 이진 분류 (Binary classification)

 이진 분류(Binary Classification)는 어떤 문제에 대하여 두 가지 중 하나를 결정하는 문제이다. 메일이 스팸메일인지 아닌지, 페이스북 피드를 보여줄지 말지, 방금 진행한 신용카드 거래가 사기인지 아닌지 판단하는 것이 이진 분류의 예다. 일반적으로 결정해야할 두 가지 결과는 0, 1로 인코딩해 사용한다.

 

# 로지스틱 회귀 (Logistic Regression)

 1. 로지스틱 회귀와 시그모이드(Sigmoid) 함수

  이진 분류를 가장 잘 해결할 수 있는 방법으로 로지스틱 회귀(Logistic Regression)가 있다. 기존의 선형 회귀는 시험에 통과할 사람을 정확히 예측하는게 어렵고, 입력값이 커질수록 출력값이 0~1 범위를 크게 벗어나 결과를 두 가지로 분류하기 어렵다. 이러한 출력값을 0~1 범위로 압축하는 함수를 이용해 출력값을 분류하는 것이 로지스틱 회귀이다.

 

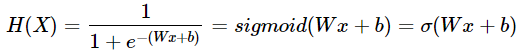
  로지스틱 회귀에서는 0~1 범위로 출력값을 압축하는 함수로 시그모이드(Sigmoid) 함수를 사용한다. 시그모이드 함수는 모든 출력값이 0~1 사이에서 나오는 특징이 있다. 이를 통해, 기존 가설인 선형 회귀에 시그모이드 함수를 덧입혀 이진 분류에 적합한 새로운 가설 H(x)를 만들 수 있다.

 

 2. 로지스틱 회귀의 Cost 함수

 

  기존 선형 회귀의 cost 함수는 기울기가 0이 되는 값이 하나여서 쉽게 최솟값을 찾을 수 있었지만, 로지스틱 회귀의 경우 비선형 함수인 sigmoid 함수로 인해 cost 함수가 훨씬 구불구불한 형태를 띄게 된다. 이로 인해, 기울기가 0이 되는 지점이 많아져 시작점에 따라 경사하강법으로 찾는 최솟값의 지점이 달라진다. 즉, cost 함수의 진짜 최솟값을 찾는 것이 어렵다.

 

  이를 극복하기 위해, 로지스틱 회귀에서는 위와 같은 cost 함수를 사용한다. 가장 왼쪽에 있는 그래프는 y = 1일 때의 cost 함수, 그 옆에 있는 그래프는 y = 0일 때의 cost 함수이다. 시그모이드 함수로 인해 생기는 지수함수적 특성을 log 함수를 사용해 중화한 덕분에 전체적으로 포물선과 비슷한 형태를 띈다. 따라서, 최솟값 찾기가 용이하다. 

  cost 함수 그래프를 살펴보자. y = 1일 때의 그래프에서 H(x)가 1에 가까울수록(예측값이 정답에 가까울수록) cost 함수가 작아지고 H(x)가 0에 가까울수록(예측값이 틀릴수록) cost 함수가 무한대로 커진다. 반대로 y = 0일 때의 그래프에서 H(x)가 1에 가까울수록(예측값이 틀릴수록) cost 함수가 무한대로 커지고 H(x)가 0에 가까울수록(예측값이 정답에 가까울수록) cost 함수가 작아진다. 로지스틱 회귀의 cost 함수가 비용함수의 역할을 정확히 수행함을 확인할 수 있다.

  비용함수를 텐서플로우로 실제로 구현할 때는 C(H(x), y) = - ylog(H(x)) - (1 - y)log(1 - H(x)) 식을 사용한다. 위의 y = 1일 때와 y = 0일 때의 비용함수를 똑같이 표현한 같은 식이며 구현의 편의를 위해 사용한다.

 

 

본 포스팅은 김성훈 교수님의 강의

'모두를 위한 딥러닝'을 학습하고 정리한 내용을 담고 있습니다.